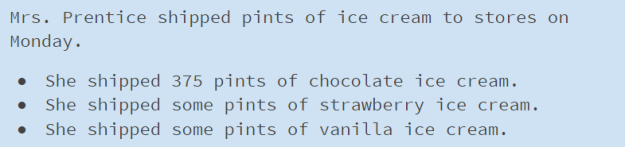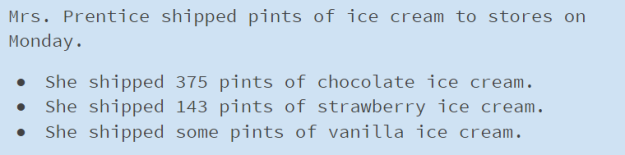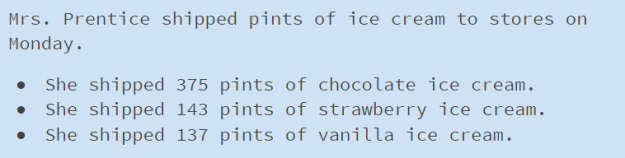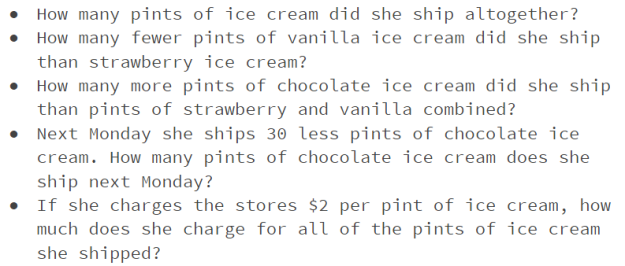Trick or Treat!

Now that I’ve completed sets of numberless word problems for all of the addition and subtraction CGI problem types, I wanted to do something fun.

This school year, my co-worker Regina Payne and I have been visiting the teachers in our Math Rocks cohort. One of the things they’ve been graciously letting us do is model how to facilitate a numberless word problems. In addition to making this a learning experience for the teachers, we’ve made it a learning experience for ourselves by putting a twist on the numberless word problem format.

Instead of your usual wordy word problem, we’ve been trying out problems that include visuals, specifically graphs. Instead of revealing numbers one at a time, we’ve been revealing parts of the graph. Let me walk you through an example I made tonight.

Here’s the graph I started with. I created it with some data I found on the Internet.

If I threw this graph at a 4th or 5th grader along with a word problem, they would probably ignore what the graph is all about and just focus on getting the numbers they need for doing whatever computations they’ve decided to do. They would probably also ignore a vital piece of information – the scale that says “In Millions” – which means their answer is going to be about 1,000,000 times too small.

But what if we could change that by starting with something a little more accessible like this?

What do you notice? What do you wonder?

I’m guessing at least one student in the class would comment that it looks like a bar graph. Interesting. What do you think this bar graph could represent?

Oh, and you think a bar is missing in the middle. Interesting. What makes you say that?

What new information was added to the graph? How does it change your thinking?

Oh, so there is a bar between Hershey’s and M&M’s. How tall do you think the bar for Snickers might be? Why do you say that?

Now we know how tall the bar for Snickers is. How does that compare to our predictions?

Considering everything we know so far, what do you think this bar graph is about? What other information do we need in order to get the full story of this graph?

What new information was added to the graph? How does it change your thinking about what this graph is about?

What are Sales? How do they relate to candy?

What does “In Millions” mean? How does that relate to Sales?

I know we don’t have any numbers yet, but what relationships do you see in the graph? What comparisons can you make?

What new information was added? How does it change your thinking?

Hmm, how many dollars in sales do you think each bar represents? How did you decide?

How do the actual numbers compare to your estimates?

What were the total sales for Reese’s in 2013? (I’d sneak in this question if I felt like the students needed a reminder about the scale being in millions.)

What are some other questions you could use answer using the data in this bar graph?

What is this question asking?

How can you use the information in the graph to help you answer this question?

*****

I may or may not actually show that last slide. After reading this blog post by one of our instructional coaches Leilani Losli, I like the idea of letting the students generate and answer their own questions. In addition to being motivating for the students, it makes my time creating the graph well spent. I don’t want to spend a lot of time digging up data, making a graph, and then asking my students a whopping one question about it! That doesn’t motivate me to make more graphs. I  also want students to recognize that we can ask lots of different questions to make sense of data to better understand the story its telling.

Some thoughts before I close. This takes longer than your typical numberless word problem. There are a lot more reveals. Don’t be surprised if this takes you at least 15-20 minutes when you take into account all of the discussion. When I first do a graphing problem like this with a class, it’s worth the time. I like the extra scaffolding. Kids without a lot of sense making practice tend to be pretty terrible about paying attention to details in graphs, especially if their focus is on solving an accompanying word problem.

If I were to use this type of problem more frequently with a group of students, I could probably start to get away with fewer and fewer reveals. Remember, the numberless word problem routine is a scaffold not a crutch. My hope is that over time the students will develop good habits for attending to features and data in graphs on their own. If you’re looking for a transition to scaffold away from numberless and toward independence, you might start by showing the full graph and then have students notice and wonder about it before revealing the accompanying word problem.

If you’d like to try out this problem, here’s a link to a slideshow with all of the graph reveals. You’ll notice blank slides interspersed throughout. I’ve found that if you have a clicker or mouse that has a tendency to jump ahead a slide or two, the blank slide can prevent accidental reveals. It also helps with graphs because when I snip the pictures in they aren’t always exactly the same size. If the blank slides weren’t there, you’d probably notice the slight differences immediately, but clearing the screen between reveals mitigates that problem.

Happy Halloween!

Writing Numberless Word Problems

So you came across my post on numberless word problems, you got excited by the idea, but you’re left wondering, “Where does he get the problems from?” Good question! I thought it was high time I answer it.

For starters, I try to avoid writing problems from scratch whenever possible. I can do it, and I have done it on numerous occasions, but I’ll be honest, it’s mentally exhausting if you have to write more than one or two problems in one sitting! It takes a lot of work to think of context after context for a variety of math topics, especially if you don’t want to feel like you’re reusing the same context over and over again.

I’ll let you in on a secret. More often than not, I base my questions on existing questions out in the world. I don’t reuse them wholesale, partly because I don’t want to infringe on copyright and partly because I don’t want to deprive teachers in my district of an existing problem they could be using with their students.

I always change names and numbers, and as needed I tweak the contexts and questions. This is so much easier than writing problems from scratch! Basing my problems on existing problems makes me feel like I’m starting 10-20 steps ahead of where I would have otherwise!

I’ll share a few problems I’ve created to give you an idea of what I’m talking about. I based all three of them off grade 3 2015 STAAR sample questions released by the Texas Education Agency.

Problem 1

Here’s the original problem:

 

First, I thought about how I could adjust the problem to make it my own:

• I decided to change the character to Jenise.
• I changed “flowers” to “carrot plants.”
• I changed 21 to 24. I did this intentionally because 24 has so many factors. You’ll see how this plays out when you get to the sample questions I created later.
• I removed the number 3 altogether. Again, this plays out later when I created questions about the situation.

Note: This step is only necessary if you want to create a unique problem. The released tests are free to be used, so you could just as easily convert this exact problem into a numberless word problem. Again, I don’t want to steal resources from my teachers so I’m opting to change this into a new problem.

Next, I think about how I want to scaffold presenting the information in the problem. I create slides, one for each phase of revealing information. Remember, the purpose of a numberless word problem is to give students an opportunity to collaboratively identify and make sense of mathematical relationships in a situation before being presented with a question. There are several factors that dictate how much or how little new information to present on each slide:

• Students’ attention span
• Students’ familiarity with the type of situation being presented
• Students’ familiarity with the math concepts involved in the situation

Here’s how I broke down this question into 4 slides:

Slide 1

Slide 2

Slide 3

Slide 4

Thinking this would be used in a 3rd grade classroom, I opted to break it down quite a bit to draw emphasis on the language of “rows” and “same number in each row.” If I already knew my students were comfortable connecting this language to multiplication and division, then I probably would have combined slides 2 and 3 into one slide.

At this point, I stop and think about what question I want to ask about the full situation on slide 4. If I were a teacher, I might select a question and keep it in my pocket. After discussing slide 4, I’d ask my students what questions they think could be asked about this situation. Students need opportunities to generate problems for themselves, not just be told the problems we expect them to solve. I could allow them to answer their own question before answering the one I had planned (or instead of!).

Here are a few questions I generated that I might ask about this situation:

This is where changing 21 to 24 in the problem adds some richness to the potential questions I could ask about this situation. This is also the reason I removed the number 3 from the original problem. Not specifying the number of rows allowed me more flexibility to ask about either the number of rows or the number of plants in each row.

Problem 2

Here’s the original problem:

I like this problem, so I didn’t want to change it too much. Here are the changes I decided to make. Remember, I always change names and numbers; context and question are tweaked as necessary.

• I changed the character to Mrs. Prentice.
• I changed the food from “yoghurt cups” to “pints of ice cream.”
• I changed the flavors to chocolate, strawberry, and vanilla.
• I changed all three numbers. However, I noted that there was a way to make ten (6 + 4) in the ones, tens, and hundreds places across the 3 numbers, so I tried to create a similar structure in my numbers with 3 + 7.

With those changes, here’s how I scaffolded the problem across 5 slides:

Slide 1

Slide 2

Slide 3

Slide 4

Slide 5

Depending on my students, I might have combined slides 4 and 5. Keeping them separate means I can play it safe. I can reveal each number one at a time, but I can also breeze through slides 3 and 4 if the situation warrants it and spend more time talking about all three numbers on slide 5.

And finally, it’s time to think of some potential questions that can be asked about this situation:

By the way, this is a great time to point out that I don’t have to pick just one! I spent valuable time crafting the situation and my students will spend valuable time making sense of the situation. Milk it for all it’s worth!

I could pose one question today for students to solve and discuss. Tomorrow we could revisit the same situation, maybe just talking about slide 5 together to jog our memories, and then I could give them another question to solve about this situation. I could even pose 2-3 questions and let the students choose which one they want to solve. Be creative!

Problem 3

Here’s the original problem:

I like this one because I’m able to take a 3rd grade problem and make it fit concepts for grades 3-5. In this case, I didn’t change as much of the original problem because the context is so simple. Here are the 3 slides I created to scaffold presenting the information:

Slide 1

Slide 2

Slide 3

It’s important to remember that the power of a numberless word problem lies in the conversation students have as you reveal each new piece of information. That conversation is driven by the questions you ask as more and more information is revealed. Here are sample questions you could use as you discuss each slide of a numberless word problem:

• What do you know?
• What information have you been given?
• What do you understand about the information given?
• What kind of problem could this be?
• What information do you know now?
• Does this new information help you?
• What does the new information tell you?
• How does the new information change or support your thinking?
• What operation(s) does this situation make you think about?
• What kinds of questions could be asked about this situation? (This can be asked on several slides, not just the final one.)

The fun part for this particular situation was thinking of all the different questions I could ask:

So there you have it – three very different examples of numberless word problems. As cool as I think numberless word problems are, please note that not every problem needs to be a numberless word problem. We have to be intentional about when and how much we provide scaffolding to our students. However, knowing about this type of problem is a great tool to have in your belt when you’re looking for ways to help your students develop a deeper understanding of the mathematical relationships in real life situations.

If you have any questions, please don’t hesitate to ask in the comments!

[UPDATE – I’ve made a page on my blog devoted to numberless word problems. Check it out for more resources.]

 

Numberless Word Problems

“They just add all the numbers. It doesn’t matter what the problem says.”

This is what a third grade teacher told my co-worker Regina Payne while she was visiting her classroom as an instructional coach. She didn’t really believe that the kids would do that, so she had the class come sit on the carpet and gave them a word problem. Sure enough, kids immediately pulled numbers out of the problem and started adding.

She thought to herself, “Oh no. I have to do something to get these kids to think about the situation.”

She brainstormed for a few moments, opened up Powerpoint, and typed the following:

Some girls entered a school art competition. Fewer boys than girls entered the competition.

She projected her screen and asked, “What math do you see in this problem?”

Pregnant pause.

“There isn’t any math. There aren’t any numbers.”

She smiles. “Sure there’s math here. Read it again and think about it.”

Finally a kid exclaims, “Oh! There are some girls. That means it’s an amount!”

“And there were some boys, too. Fewer boys than girls,” another child adds.

“What do you think fewer boys than girls means?” she asks.

“There were less boys than girls,” one of the students responds.

“Ok, so what do we know already?”

“There were some girls and boys, and the number of boys is less than the number of girls.”

“Look at that,” she points out, “All that math reasoning and there aren’t even any numbers in the problem. How many boys and girls could have entered into the competition?”

At this point the students start tossing out estimates, but the best part is that their estimates are based on the mathematical relationship in the problem. If a student suggested 50 girls, then the class knew the number of boys had to be an amount less than 50. If a student suggested 25 girls, then the number of boys drops to an amount less than 25.

When it seems like the students are ready, she makes a new slide that says:

135 girls entered a school art competition. Fewer boys than girls entered the competition.

Acting very curious, she asks, “Hmm, does this change what we know at all?”

A student points out, “We know how many girls there are now. 135 girls were in the competition.”

“So what does that tell us?”

Another student responds, “Now that we know how many girls there are, we know that the number of boys is less than 135.”

This is where the class starts a lively debate about how many boys there could be. At first the class thinks it could be any number from 0 up to 134. But then some students start saying that it can’t be 0 because that would mean no boys entered the competition. Since it says fewer boys than girls, they take that to mean that at least 1 boy entered the competition. This is when another student points out that actually the number needs to be at least 2 because it says boys and that is a plural noun.

Stop for a moment. Look at all this great conversation and math reasoning from a class that moments before was mindlessly adding all the numbers they could find in a word problem?

Once the class finishes their debate about the possible range for the number of boys, my co-worker shows them a slide that says:

135 girls entered a school art competition. Fifteen fewer boys than girls entered the competition.

“What new information do you see? How does it change your understanding of the situation?”

“Now we know something about the boys,” one of the students replies.

“Yeah, we know there are 15 boys,” says another.

“No, there are 15 fewer, not 15.”

Another debate begins. Some students see 15 and immediately go blind regarding the word fewer. It takes some back and forth for the students to convince each other that 15 fewer means that the number of boys is not actually 15 but a number that is 15 less than the number of girls, 135.

To throw a final wrench in to the discussion, she asks, “So what question could I ask you about this situation?”

To give you a heads up, after presenting to this one class she ended up repeating this experience in numerous classrooms across our district. After sharing it with hundreds of students, only one student out of all of them ever guessed the question she actually asked.

Do you think you know what it is? Can you guess what the students thought it would be?

I’ll give you a moment, just in case.

So all but one student across the district guessed, “How many boys entered the art competition?”

That of course is the obvious question, so instead she asked, “How many children entered the art competition?”

Young minds, completely blown.

At first there were cries of her being unfair, but then they quickly got back on track figuring out the answer using their thorough understanding of the situation.

And that is how my co-worker got our district to start using what she dubbed Numberless Word Problems – a scaffolded approach to presenting word problems that gets kids thinking before they ever have numbers or a question to act on.

Recently we shared this strategy with our district interventionists and several of them went off and tried it that week. They wrote back sharing stories of how excited and engaged their students were in solving problems that would have seemed too difficult otherwise. This seems like a great activity structure for struggling students because it starts off in a nonthreatening way – no numbers, how ’bout that? – and lets them build confidence before they ever have to solve anything.

Do I think that every word problem should be presented this way? No. But I do think this is a great way to prompt rich discussion and get students to notice and grapple with the relationships in problem situations and to observe how the language helps us understand those relationships. To me this is a scaffold that can help get students to attend to information and language. As many teachers like to say, standardized tests are as much reading tests as they are math tests.

Perhaps you can use this activity structure when students are seeing a new problem type for the first time and then fade away from using it over time. Or maybe you have students who have been doing great understanding word problems, but lately they’re rushing through them and making careless errors. This might be an opportunity to use this structure to slow them down and get them thinking again.

Either way, if you do try this out, I’d love to hear how it went.

[UPDATE 1: I wrote a follow up post about writing numberless word problems if you’d like to learn more.]

[UPDATE 2: I’ve created a page on my blog devoted to numberless word problems. Check it out for more resources.]