Writing Numberless Word Problems

So you came across my post on numberless word problems, you got excited by the idea, but you’re left wondering, “Where does he get the problems from?” Good question! I thought it was high time I answer it.

For starters, I try to avoid writing problems from scratch whenever possible. I can do it, and I have done it on numerous occasions, but I’ll be honest, it’s mentally exhausting if you have to write more than one or two problems in one sitting! It takes a lot of work to think of context after context for a variety of math topics, especially if you don’t want to feel like you’re reusing the same context over and over again.

I’ll let you in on a secret. More often than not, I base my questions on existing questions out in the world. I don’t reuse them wholesale, partly because I don’t want to infringe on copyright and partly because I don’t want to deprive teachers in my district of an existing problem they could be using with their students.

I always change names and numbers, and as needed I tweak the contexts and questions. This is so much easier than writing problems from scratch! Basing my problems on existing problems makes me feel like I’m starting 10-20 steps ahead of where I would have otherwise!

I’ll share a few problems I’ve created to give you an idea of what I’m talking about. I based all three of them off grade 3 2015 STAAR sample questions released by the Texas Education Agency.

Problem 1

Here’s the original problem:

 

First, I thought about how I could adjust the problem to make it my own:

• I decided to change the character to Jenise.
• I changed “flowers” to “carrot plants.”
• I changed 21 to 24. I did this intentionally because 24 has so many factors. You’ll see how this plays out when you get to the sample questions I created later.
• I removed the number 3 altogether. Again, this plays out later when I created questions about the situation.

Note: This step is only necessary if you want to create a unique problem. The released tests are free to be used, so you could just as easily convert this exact problem into a numberless word problem. Again, I don’t want to steal resources from my teachers so I’m opting to change this into a new problem.

Next, I think about how I want to scaffold presenting the information in the problem. I create slides, one for each phase of revealing information. Remember, the purpose of a numberless word problem is to give students an opportunity to collaboratively identify and make sense of mathematical relationships in a situation before being presented with a question. There are several factors that dictate how much or how little new information to present on each slide:

• Students’ attention span
• Students’ familiarity with the type of situation being presented
• Students’ familiarity with the math concepts involved in the situation

Here’s how I broke down this question into 4 slides:

Slide 1

Slide 2

Slide 3

Slide 4

Thinking this would be used in a 3rd grade classroom, I opted to break it down quite a bit to draw emphasis on the language of “rows” and “same number in each row.” If I already knew my students were comfortable connecting this language to multiplication and division, then I probably would have combined slides 2 and 3 into one slide.

At this point, I stop and think about what question I want to ask about the full situation on slide 4. If I were a teacher, I might select a question and keep it in my pocket. After discussing slide 4, I’d ask my students what questions they think could be asked about this situation. Students need opportunities to generate problems for themselves, not just be told the problems we expect them to solve. I could allow them to answer their own question before answering the one I had planned (or instead of!).

Here are a few questions I generated that I might ask about this situation:

This is where changing 21 to 24 in the problem adds some richness to the potential questions I could ask about this situation. This is also the reason I removed the number 3 from the original problem. Not specifying the number of rows allowed me more flexibility to ask about either the number of rows or the number of plants in each row.

Problem 2

Here’s the original problem:

I like this problem, so I didn’t want to change it too much. Here are the changes I decided to make. Remember, I always change names and numbers; context and question are tweaked as necessary.

• I changed the character to Mrs. Prentice.
• I changed the food from “yoghurt cups” to “pints of ice cream.”
• I changed the flavors to chocolate, strawberry, and vanilla.
• I changed all three numbers. However, I noted that there was a way to make ten (6 + 4) in the ones, tens, and hundreds places across the 3 numbers, so I tried to create a similar structure in my numbers with 3 + 7.

With those changes, here’s how I scaffolded the problem across 5 slides:

Slide 1

Slide 2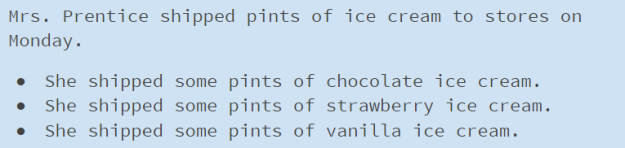

Slide 3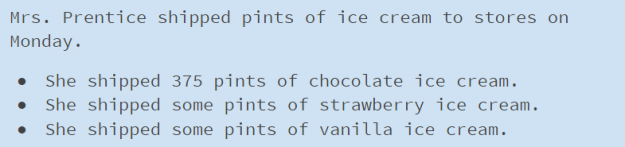

Slide 4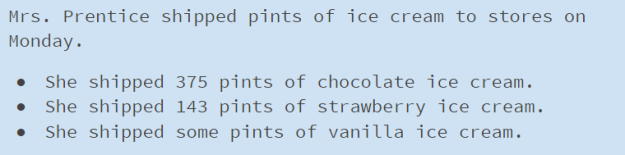

Slide 5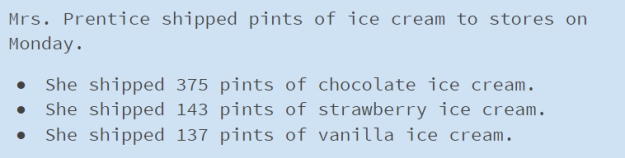

Depending on my students, I might have combined slides 4 and 5. Keeping them separate means I can play it safe. I can reveal each number one at a time, but I can also breeze through slides 3 and 4 if the situation warrants it and spend more time talking about all three numbers on slide 5.

And finally, it’s time to think of some potential questions that can be asked about this situation:

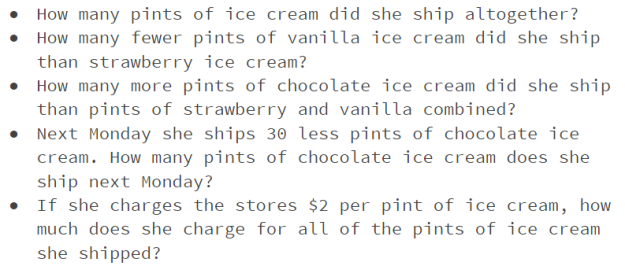
By the way, this is a great time to point out that I don’t have to pick just one! I spent valuable time crafting the situation and my students will spend valuable time making sense of the situation. Milk it for all it’s worth!

I could pose one question today for students to solve and discuss. Tomorrow we could revisit the same situation, maybe just talking about slide 5 together to jog our memories, and then I could give them another question to solve about this situation. I could even pose 2-3 questions and let the students choose which one they want to solve. Be creative!

Problem 3

Here’s the original problem:

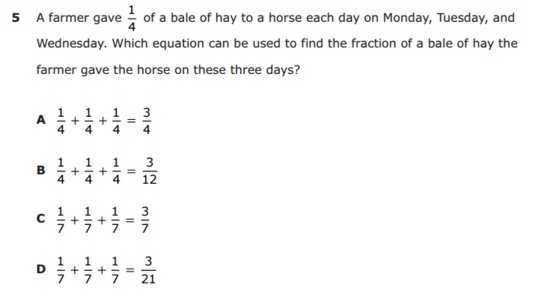
I like this one because I’m able to take a 3rd grade problem and make it fit concepts for grades 3-5. In this case, I didn’t change as much of the original problem because the context is so simple. Here are the 3 slides I created to scaffold presenting the information:

Slide 1

Slide 2

Slide 3

It’s important to remember that the power of a numberless word problem lies in the conversation students have as you reveal each new piece of information. That conversation is driven by the questions you ask as more and more information is revealed. Here are sample questions you could use as you discuss each slide of a numberless word problem:

• What do you know?
• What information have you been given?
• What do you understand about the information given?
• What kind of problem could this be?
• What information do you know now?
• Does this new information help you?
• What does the new information tell you?
• How does the new information change or support your thinking?
• What operation(s) does this situation make you think about?
• What kinds of questions could be asked about this situation? (This can be asked on several slides, not just the final one.)

The fun part for this particular situation was thinking of all the different questions I could ask:

So there you have it – three very different examples of numberless word problems. As cool as I think numberless word problems are, please note that not every problem needs to be a numberless word problem. We have to be intentional about when and how much we provide scaffolding to our students. However, knowing about this type of problem is a great tool to have in your belt when you’re looking for ways to help your students develop a deeper understanding of the mathematical relationships in real life situations.

If you have any questions, please don’t hesitate to ask in the comments!

[UPDATE – I’ve made a page on my blog devoted to numberless word problems. Check it out for more resources.]