Writing Numberless Word Problems

So you came across my post on numberless word problems, you got excited by the idea, but you’re left wondering, “Where does he get the problems from?” Good question! I thought it was high time I answer it.

For starters, I try to avoid writing problems from scratch whenever possible. I can do it, and I have done it on numerous occasions, but I’ll be honest, it’s mentally exhausting if you have to write more than one or two problems in one sitting! It takes a lot of work to think of context after context for a variety of math topics, especially if you don’t want to feel like you’re reusing the same context over and over again.

I’ll let you in on a secret. More often than not, I base my questions on existing questions out in the world. I don’t reuse them wholesale, partly because I don’t want to infringe on copyright and partly because I don’t want to deprive teachers in my district of an existing problem they could be using with their students.

I always change names and numbers, and as needed I tweak the contexts and questions. This is so much easier than writing problems from scratch! Basing my problems on existing problems makes me feel like I’m starting 10-20 steps ahead of where I would have otherwise!

I’ll share a few problems I’ve created to give you an idea of what I’m talking about. I based all three of them off grade 3 2015 STAAR sample questions released by the Texas Education Agency.

Problem 1

Here’s the original problem:

 

First, I thought about how I could adjust the problem to make it my own:

• I decided to change the character to Jenise.
• I changed “flowers” to “carrot plants.”
• I changed 21 to 24. I did this intentionally because 24 has so many factors. You’ll see how this plays out when you get to the sample questions I created later.
• I removed the number 3 altogether. Again, this plays out later when I created questions about the situation.

Note: This step is only necessary if you want to create a unique problem. The released tests are free to be used, so you could just as easily convert this exact problem into a numberless word problem. Again, I don’t want to steal resources from my teachers so I’m opting to change this into a new problem.

Next, I think about how I want to scaffold presenting the information in the problem. I create slides, one for each phase of revealing information. Remember, the purpose of a numberless word problem is to give students an opportunity to collaboratively identify and make sense of mathematical relationships in a situation before being presented with a question. There are several factors that dictate how much or how little new information to present on each slide:

• Students’ attention span
• Students’ familiarity with the type of situation being presented
• Students’ familiarity with the math concepts involved in the situation

Here’s how I broke down this question into 4 slides:

Slide 1

Slide 2

Slide 3

Slide 4

Thinking this would be used in a 3rd grade classroom, I opted to break it down quite a bit to draw emphasis on the language of “rows” and “same number in each row.” If I already knew my students were comfortable connecting this language to multiplication and division, then I probably would have combined slides 2 and 3 into one slide.

At this point, I stop and think about what question I want to ask about the full situation on slide 4. If I were a teacher, I might select a question and keep it in my pocket. After discussing slide 4, I’d ask my students what questions they think could be asked about this situation. Students need opportunities to generate problems for themselves, not just be told the problems we expect them to solve. I could allow them to answer their own question before answering the one I had planned (or instead of!).

Here are a few questions I generated that I might ask about this situation:

This is where changing 21 to 24 in the problem adds some richness to the potential questions I could ask about this situation. This is also the reason I removed the number 3 from the original problem. Not specifying the number of rows allowed me more flexibility to ask about either the number of rows or the number of plants in each row.

Problem 2

Here’s the original problem:

I like this problem, so I didn’t want to change it too much. Here are the changes I decided to make. Remember, I always change names and numbers; context and question are tweaked as necessary.

• I changed the character to Mrs. Prentice.
• I changed the food from “yoghurt cups” to “pints of ice cream.”
• I changed the flavors to chocolate, strawberry, and vanilla.
• I changed all three numbers. However, I noted that there was a way to make ten (6 + 4) in the ones, tens, and hundreds places across the 3 numbers, so I tried to create a similar structure in my numbers with 3 + 7.

With those changes, here’s how I scaffolded the problem across 5 slides:

Slide 1

Slide 2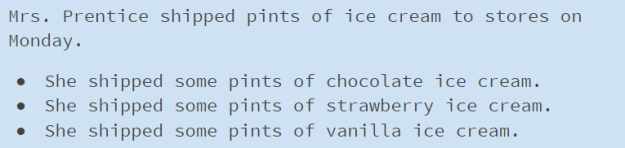

Slide 3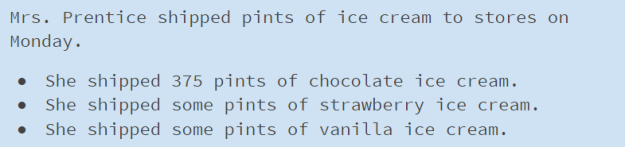

Slide 4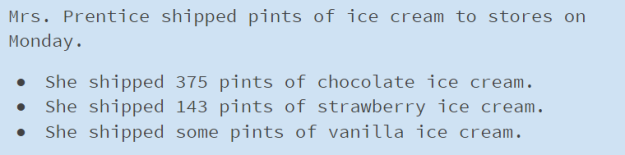

Slide 5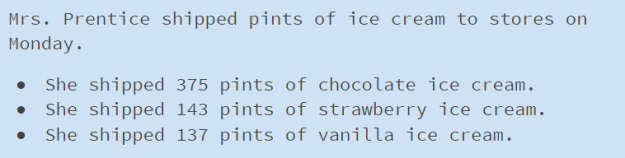

Depending on my students, I might have combined slides 4 and 5. Keeping them separate means I can play it safe. I can reveal each number one at a time, but I can also breeze through slides 3 and 4 if the situation warrants it and spend more time talking about all three numbers on slide 5.

And finally, it’s time to think of some potential questions that can be asked about this situation:

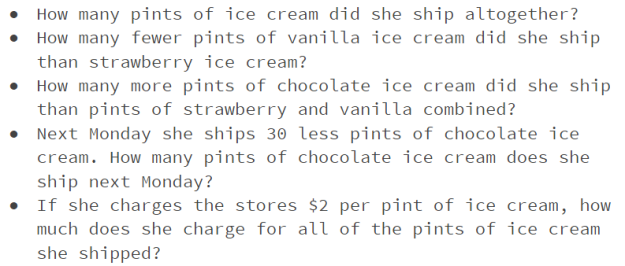
By the way, this is a great time to point out that I don’t have to pick just one! I spent valuable time crafting the situation and my students will spend valuable time making sense of the situation. Milk it for all it’s worth!

I could pose one question today for students to solve and discuss. Tomorrow we could revisit the same situation, maybe just talking about slide 5 together to jog our memories, and then I could give them another question to solve about this situation. I could even pose 2-3 questions and let the students choose which one they want to solve. Be creative!

Problem 3

Here’s the original problem:

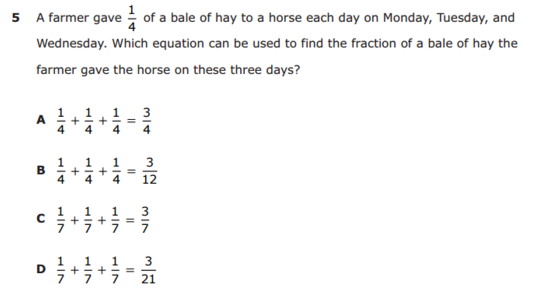
I like this one because I’m able to take a 3rd grade problem and make it fit concepts for grades 3-5. In this case, I didn’t change as much of the original problem because the context is so simple. Here are the 3 slides I created to scaffold presenting the information:

Slide 1

Slide 2

Slide 3

It’s important to remember that the power of a numberless word problem lies in the conversation students have as you reveal each new piece of information. That conversation is driven by the questions you ask as more and more information is revealed. Here are sample questions you could use as you discuss each slide of a numberless word problem:

• What do you know?
• What information have you been given?
• What do you understand about the information given?
• What kind of problem could this be?
• What information do you know now?
• Does this new information help you?
• What does the new information tell you?
• How does the new information change or support your thinking?
• What operation(s) does this situation make you think about?
• What kinds of questions could be asked about this situation? (This can be asked on several slides, not just the final one.)

The fun part for this particular situation was thinking of all the different questions I could ask:

So there you have it – three very different examples of numberless word problems. As cool as I think numberless word problems are, please note that not every problem needs to be a numberless word problem. We have to be intentional about when and how much we provide scaffolding to our students. However, knowing about this type of problem is a great tool to have in your belt when you’re looking for ways to help your students develop a deeper understanding of the mathematical relationships in real life situations.

If you have any questions, please don’t hesitate to ask in the comments!

[UPDATE – I’ve made a page on my blog devoted to numberless word problems. Check it out for more resources.]

 

Better Questions: Math Rocks Meets Open Middle

This year I have been leading a cohort of elementary math educators in my district. We met for two full days in July – you can read about that here and here – and throughout this school year we’ve met every other Thursday after school.

In December, our meeting focused on the work of Robert Kaplinsky, specifically his IGNITE talk about productive struggle and his website openmiddle.com.

At the start of the session, everyone reflected on what “productive struggle” means to them. This is important because as certain phrases become popular in education, they quickly become jargon. I wanted to ensure everyone had a chance to think about how they interpret the phrase and share that with the group. Then we watched Robert’s IGNITE talk.

The image that stood out most to me from his talk was the one of the mom riding the bike for her child. It seems so silly, and yet there are many instances as teachers where we can find ourselves doing the thinking for our students instead of letting them try either on their own or with our support.

At the end of the video, Robert puts out a call to action for teachers to create opportunities for students to productively struggle. And why not start by having the Math Rocks participants do some productive struggling of their own? Regina and I posted 10 problems around the room. We let everyone loose to do some math for 15 minutes. They dove right in!

All 10 problems came from openmiddle.com. If you aren’t familiar with the open middle problem type, here’s a brief summary: (You can learn more here.)

• they have a “closed beginning” meaning they all start with the same initial problem
• they have a “closed end” meaning that they all end with the same answer
• they have an “open middle” meaning there are multiple ways to approach and ultimately solve the problem

After debriefing as a group and sharing information about open middle problems, we came back around to the idea of productive struggle with this video from Michael Pershan. The whole thing is interesting, but for the purposes of our discussion, we watched the first 30 seconds of the video, and then we watched from 1:45 to 5:45.

By this point, we had made our case and it was time for the participants to take a stab at designing their own open middle problems. They had a choice of writing one from scratch or taking an existing problem from our curriculum and redesigning it as an open middle problem. A nice surprise is that our adopted textbook, Stepping Stones, already uses open middle problems in many lessons and activities! They don’t name them as such, but that’s essentially what they are.

We shared out the open middle problems they wrote. Afterward we gathered them together in this document if you’d like to see our first attempts. We closed the session with their homework assignment – giving their students an open middle problem and reflecting on it in a blog post. If you’re interested in learning more about open middle problems – especially learning from teachers trying them out for the first time! – check out our open middle blog post collection.

The consensus from the group seems to be that they can initially throw kids off if they’re not used to being asked questions like this, especially for those kids who want to neatly and easily come to the correct answer, but the questions provide opportunities for the type of thinking and struggling we want our students to engage in and we need to be using them more often.

Flipping the Flipped Classroom

Source: ransomtech (CC BY-NC-SA 2.0)

In an earlier post I questioned the trendy use of foldables. Today I want to question the flipped classroom model which is all the rage right now. If you’re somehow unfamiliar with this model, here’s a handy infographic you should check out.

So the basic premise of the flipped classroom is that the lecture portion of instruction is recorded in some way and students watch this lecture on computers at home for homework. Then, in class, the students work on more engaging activities (practice) because they’ve already “learned” the content of the lesson at home. The teacher, free from having to lecture, is able to walk around and help students with problems as they arise. Educators like to talk about transitioning their role from the “sage on the stage” to the “guide on the side” and this model definitely allows for that transition in roles…in the classroom only.

Here is my primary concern:

What is with the insistence on the lecture (direct instruction) model?

Teachers appear to be loving the ability to offer more engaging, open-ended activities in class now that students are watching lectures at home.

What was stopping these teachers from offering these kinds of activities before?

Why do teachers think students have to be told what to do before they actually do any math?

The use of instructional videos as “pre-learning” shows that the transmission model of education is in no danger of going away. In all these years, hasn’t the field of education learned enough about how students learn best to know that talking at them is not ideal? Don’t get me wrong, having access to these kinds of videos as a resource is great. If I’m working out a problem, and I realize I need to brush up on the Pythagorean theorem, then watching a 5-7 minute video might be super helpful. Why do we assume students need to be told everything they need to know about a concept or a strategy before trying out a problem or two for themselves?

Flipping the Flipped Classroom

If anything, I would rather suggest flipping the classroom in the other direction. First, start with an engaging problem. Look at Dan Meyer’s three act problems for one approach. Don’t spend a lot of time talking at your students from the get go. Have a brief discussion about the situation and then let them go. If it’s challenging, let them work in pairs or small groups to brainstorm together. If they finish quickly, give them some other problems related to the big idea of the lesson. Finally, pull the class together and debrief. Talk. Have discussion, not lecture. At this point, if you want to tell the students something, they are much more receptive to hearing it and asking questions about it. I have witnessed this first hand. Students are more talkative after engaging with content, not before. Students love to think and talk, but they are more readily engaged if they have some connection with what you’re talking about. And if you still want to make an instructional video, great! The students have struggled with the content, they’ve talked about it with each other, and they’ve talked about it with you. Watching a video might help cement ideas that they weren’t quite sure about yet.

With this model you’re showing students that they can learn content without having to be told exactly what steps to take. Instead the role of a student is being problem solvers engaged in their own learning and processes, rather than passive recipients of information that may or may not “stick” or that they may not understand how to apply.

Folding big ideas into little origami

Source: Mike Baker (CC BY-NC-SA 2.0)

I read a blog post by Grant Wiggins today that got me thinking. When I first read the post, I thought it was extremely long-winded, but even still the message resonated with me, and I’ve been mulling it over ever since.

The gist of his piece is that too much is done in schools without asking the hard questions (or acting on them even if we are asking them).

• Why are we teaching what we are teaching?
• Why are we using the methods we are using?
• Are they the best way?
• Could they be better?
• What are my assumptions about my teaching? About my students?
• What are the unintended consequences of my actions?

Lately I’ve seen this topic repeatedly in blog posts and on Twitter. With its popularity, it seems apropos to question it:

Why are teachers using so many foldables as part of their instruction?

What are they adding to the students’ learning? Do the students understand why they are using these tools? Do they even realize they are tools? What are the unintended consequences of folding big ideas into so many different shapes of origami?

I’m not going to try to answer the question myself, at least not today. And by asking, don’t think I’m against them. I just want to pose the question because I think it’s worth asking. I’m sure folded things have been used in classrooms for decades, but they have seen a spike in popularity in recent years. Beyond being incredibly clever in and of themselves, what good are they doing for student learning? What harm?

To question, how to question, that is the question…or something

Source: Colin Kinner (CC BY 2.0)

Yesterday I read a post called Questions and more questions! on the blog in stillness the dancing. [UPDATE – Beth Ferguson (@algebrasfriend) updated and revised this post in 2016. You can check out the updated version here.]

After reading the post, I ended up writing a comment with the thoughts that came to my mind about questioning. After I posted it, I thought about how I had read a lot of great blog posts throughout the day, and I comment on a lot of them! I really enjoy thinking about what people have to say and sharing my thoughts in return. What I realized is that one of the primary purposes of this blog I just created is for personal reflection and a place to store my thoughts. So, going forward, I’m going to start copy and posting some of those thoughts here so I capture them rather than cast them about the blogosphere like seeds in the wind. Of course, I’m honored if any of my thoughts are the seed of a conversation elsewhere, but I don’t want to ignore my little garden patch of ideas here on my blog.

So, without further ado, and to extract myself from the gardening metaphor I stumbled into, here’s what I want to remember I said after reading the post on questioning. (And since I’m taking the time to collect it here, I’m going to organize and revise it a bit based on thoughts I had since I initially wrote the comment.)

A few tips I can give from my experiences with questioning:

1. Give away the answer. Sometimes I present a problem, and almost immediately give away the answer. That way when we’re talking about the process for finding the answer, the students aren’t hung up wondering whether they’re correct or not. Also it demonstrates that I care about more than getting the right answer. How we get the answer, especially if there is more than one solution path, means a great deal to me, and I want it to mean a great deal to my students.

2. Do your students understand the question? This may only apply to younger students, or perhaps students where English isn’t their first language, but I was surprised to find out how difficult it was for students to grasp “missing information” questions. For example, “Tom has $30. He buys some candies that cost $4 per pack. What information is needed in order to determine how much Tom spent?” It amazed me that until we had talked explicitly about this question type several times, my students (4th graders) completely ignored the part asking about missing information. They jumped right to the question, or at least what they saw as the question – How much did Tom spend? They couldn’t grasp that this question was impossible to solve without more information. It goes to show how much understanding language is wrapped up in understanding math.

3. Let students write the questions. I like providing students situations with lots of information and asking students to pose the questions we might solve based on this information. For example, I read a blog today where someone posted a worksheet showing the writer’s times on various legs of a triathlon. She also included her friend’s times on the same triathlon. The question she posed was whether she and her friend finished at the same time. I like the question, but after looking at the data, I couldn’t help but think of all the other questions you could ask using that same data. Students have to make all sorts of connections to their prior knowledge to look at a set of data and think of questions to ask. Of course they’ll likely start with very obvious questions, but with practice they can get very creative!

4. Ask, “Are you sure?” even if they’re right! Students are pretty smart. They realize that adults often ask this question to indicate that the student has made a mistake. Teachers should be asking this question regardless of whether the answer is correct or not. If you want a student to be confident in their answer, and more importantly if they want to be confident in their answers, this is a question they should hear repeatedly and learn to ask themselves.

5. Be a traffic cop. When you ask a question and a student answers, you can stop all momentum by saying, “Correct,” and moving on. But imagine if you say instead, “Oh, Zaida thinks the answer is 24. John, do you agree or disagree with this answer?” followed by, “Oh, John says he agrees with the answer of 24. Mary, why do you think both students are saying the answer is 24?” The student answers pass through you but you immediately pass direct them in the form of a new question to another student in the class. You don’t have to do this if the question is simple. If I’m teaching 5^th graders and for some reason I ask the sum of 12 + 12, then I’m not going to engage in a lengthy discussion, but if the students are evaluating a situation using concepts we’re currently working on, then you better believe we’re going to talk it out, and they’re not going to think the answer is correct because I told them so, but because we built consensus as a class.

So those are my thoughts on questioning that I wanted to capture. I love getting involved in conversations with students and questioning them to learn more about their thinking and how they approached a problem. It fascinates me what goes in the brains of kids. They can be surprisingly clever and sophisticated; we just have to give them opportunities to show us how cool their thinking is.